闘技場の豆知識 カードの出現確率
闘技場に役に立つかもしれない事項を公開しておきます。
基礎的な事項から応用まで。

カードプール
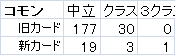
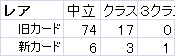
僕が数えた現在闘技場で出てくるコモンとレアのカードの個数です(パラディンの)。自分で数えたので、もしかしたらずれているかもしれません。
新カードは現在の最新拡張である"仁義なきガジェッツァン"のカードのことで、旧カードはそれ以外のカードのことです。ちょっと切れてしまったいますが、一番右は3クラスまたいだカードです。
コモン
レア
禁止カード
クトゥーン、それを補佐するカード、以下の画像のカードが禁止カードです。画像は拾いものです。どなたか分かりませんがあなたの画像は役に立っています。
上のカードプールの表は、禁止カードがないパラディンのものとなっています。別のヒーローのカードプールは、画像の禁止カードと古代の盾持ちといったクラス固有のクトゥーン系カードを除くことで分かります。
カードボーナス
最新拡張とクラスカードは、そうでないカードと比べて3択に出やすいボーナスがかかっています。古い中立カードと比べて、古いクラスカードは2倍、最新拡張の中立カードは2倍も3択に出やすいです。以下のHearthArenaというピック支援ツールを運営している人がそう言っています。
僕も個人でyoutubeやtwitchの録画を見て3択を91回記録してみました。
集計結果
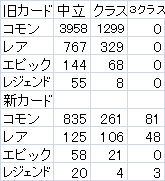
この表を元に計算すると、コモンの古いクラスカードは1.94倍、コモンの新しい中立カードは1.97倍出やすいという結果になります。よって、古いクラスカードも新しい中立カードも2倍のボーナスがかかっているのでしょう。
また、最新拡張のクラスカードは3.89倍出やすいという計算結果になったので、おそらく最新拡張のクラスカードは4倍出やすいです。
ボーナスの計算方法
興味ない人は飛ばしてください。
A=(コモンの新しい中立カードの出現枚数) ÷ (コモンの古い中立カードの出現枚数)
B=(コモンの新しい中立カードプールの枚数) ÷ (コモンの古い中立カードプールの枚数)
コモンの新しい中立カードにかかっているボーナス= A ÷ B
レア度別の出現頻度
さきほどの自分で集計したカード出現枚数を割合で見ることもできます。闘技場で1回あたりレアカードは5枚とれます。

特定1枚のカードをとる
カードプール、カードボーナス、レア度別の出現頻度をもとに、特定の1枚のカードを1回の闘技場でとれる確率を計算することができます。パラディンの場合のカードプールで計算してみましたが、どのヒーローでも大体同じです。

例えば聖別、フレイムストライク、炎の大地のポータルといったコモン(基本カード含む)の古いクラスカードは平均0.5枚とれ、40%で1枚以上とれます。
グライムストリートの道具屋、奈落の始末屋といったコモンの新しいクラスカードは平均1枚とれ、60%で1枚以上とれます。なので、平均的には3試合に1回は7ターン目に奈落の始末屋を出せる/出されることが分かります(7ターン目でデッキの1/3引くと仮定)。勝ち上がっていくと強い相手に当たるので、その時にはより高い確率で出してくるでしょう。
計算方法
興味ない人はもう帰って大丈夫です。計算方法を知りたい人のためにかいておきます。
前にやったように、倍率がかかっているカードをかさ増しして、重複なくカードを選びとっていくという考え方をします。
ドラコニッド諜報員の発見はカードの枚数によるのか? - ハースストーン丸呑み
かさ増しされた場合の数を求めます。
a=ボーナス無しのカード(古い中立)の枚数
b=2倍ボーナスのカード(古いクラス、新しい中立)の枚数
c=4倍ボーナスのカード(新しいクラス)の枚数
とおきます。
いきなり全部考えると難しいので、一部だけ考えます。ボーナス無し2枚と2倍ボーナス1枚が3択に現れるかさ増しされた場合の数は aC2 ✕ (bC1 ✕ 2) です。2倍のボーナスがかかっているので、その分2倍の場合の数があると考えます。あとはこれを全てのパターン列挙するだけです。◯^△は◯の△乗を表します。
ボーナス無しのカードのみ(3枚)を3択でとれるの場合の数=aC3
ボーナス無しのカード2枚、ボーナス無し以外から2枚=aC2 ✕ {bC1 ✕2 + cC1 ✕4}
ボーナス無しのカード1枚、ボーナス無し以外から2枚=aC1 ✕ {bC2 ✕ 2^2 + bC1 ✕2 ✕ cC1 ✕4 + cC2 ✕ 4^2}
ボーナス無し以外から3枚=bC3 ✕ 2^3 + bC2 ✕2^2 ✕ cC1 ✕4 + bC1 ✕2 ✕ cC2 ✕4^2 + cC3 ✕ 4^3
上の4つの場合の数を足せば、かさ増しされた場合の数の出来上がりです。
次に特定の1枚を選んだ時のかさ増しされた場合の数も求めます。ボーナスカードを選び出す時はちゃんとその枚数分ボーナスをかけるだけです。
(特定の1枚のボーナス無しカードがとれる場合の数)
=(残りのボーナス無しカードを2枚選ぶ場合の数)
+(残りのボーナス無しカードを1枚選ぶ場合の数)✕(ボーナス2,4倍カードを1枚選ぶ場合の数)
+(ボーナス2,4倍カードを2枚選ぶ場合の数)
=(a-1)C2
+ (a-1)C1 ✕ {bC1 ✕2 + cC1 ✕4}
+ {bC2 ✕ 2^2 + bC1 ✕2 ✕ cC1 ✕4 + cC2 ✕ 4^2}
特定の1枚のボーナス2倍カードがとれる場合の数=2 ✕ [aC2 + aC1 ✕ {(b-1)C1 ✕ 2 + cC1 ✕4} + (b-1)C2 ✕ 2^2 + (b-1)C1 ✕2 ✕ cC1 ✕4 + cC2 ✕4^2]
特定の1枚のボーナス4倍カードがとれる場合の数=4 ✕ [aC2 + aC1 ✕ {bC1 ✕ 2 + (c-1)C1 ✕4} + bC2 ✕ 2^2 + bC1 ✕2 ✕ (c-1)C1 ✕4 + (c-1)C2 ✕4^2]
場合の数を全体の場合の数で割れば、3択で特定のカードが出る確率が求まります。それを30回繰り返すのが闘技場です。以上。
